总结一下数据结构的知识,以便之后忘记了可以翻阅,哈哈,就像是做了一次备份哇
基本概念与术语
数据
是对客观事物的符号表示,很笼统的概念,范围很大
数据对象
是性质相同的数据元素的集合,是数据的子集
数据元素
是组成数据的基本单位
数据项
一个数据元素可以由若干个数据项组成
数据项是数据的不可分割的最小单位
数据结构
是相互之间存在的一种或多种特定关系的数据元素的集合
逻辑结构
是指数据对象中数据元素之间的相互关系
- 集合结构
- 线性结构
- 树形结构
- 图形结构或图状结构
物理结构
是指数据的逻辑结构在计算机中存储形式
- 顺序存储结构
- 链式存储结构
算法
解决问题的方法
特性
- 有穷性
- 确定性
- 可行性
- 输入
- 输出
时间复杂度
记作 T(n) = O(f(n))
表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,也称作渐进时间复杂度
小贴士:
这里我们学到优化程序,不单单是降低时间复杂度,还可以从空间复杂度来解决,如果不考虑容量,可以用空间换效率
线性表
顺序存储结构
1 |
|
链式存储结构
1 | typedef int ElemType; |
循环链表
表中最后的一个结点的指针域指向头结点,整个链表形成一个环
和线性链表基本一致,差别在于判断循环条件不是p或者p->next是否为空,而是它们是否等于头指针
双向链表
就是不仅仅有指向后继的指针,还有增加了指向前驱的指针
1 | typedef int ElemType; |
栈和队列
栈
后进先出 LIFO
1 | typedef struct |
栈可以在程序设计语言中实现递归(调用自己的行为叫做递归)
队列
先进先出 FIFO
1 | typedef struct QNode |
循环队列
特点
在非空队列中,头指针始终指向队列头元素,而尾指针始终指向队列尾元素的下一个位置,这样当front等于rear时,此队列不是还剩一个元素,而是空队列。
串
1 | typedef struct |
广义表
术语
长度
第一层(括号)的数量
深度
层数(括号数)
速学路径
http://www.zybang.com/question/17d8254f4028ac9695f79081f32542f4.html
树
基本术语
结点
树上的一个元素
度
结点拥有的子树数
叶子
度为0的结点
孩子
结点的子树
双亲
子树的派生数称为双亲
兄弟
同一个双亲的孩子互称兄弟
深度
树中结点的最大层次称为树的深度
森林
几棵互不相交的树的集合
二叉树
每个结点最多两棵子树的树
性质
- 在二叉树的第 i 层上最多有2^i-1^个结点
- 深度为 k 的二叉树最多有2^k^-1个结点
- 任何一棵二叉树,如果叶子结点数为n~0~,度为2的结点数为n~2~,则n~0~ = n~2~+1
- 具有n个结点的完全二叉树的深度为[log~2~n]+1
存储结构
顺序存储结构
根据完全二叉树的顺序,依次排列,形成顺序表
链式存储结构
1 | typedef struct BiTNode |
遍历二叉树
仅仅是根节点的输出顺序的前后
- 先序遍历
- 中序遍历
- 后序遍历
线索二叉树
相比二叉树,他增加了前驱和后继的元素,为了节约空间,数据位还是采用之前的左右子树,但是用tag来表示是两边的数据位是左孩子还是前驱,右孩子还是后继
| 左数据位 | 标识 | 数据 | 标识 | 右数据位 |
|---|---|---|---|---|
| Lchild | LTag | data | RTag | Rchild |
如果tag为0,表示是孩子的数据,如果为1,表示是前驱或者后继
线索化
一般用中序遍历二叉树,使其变成线索二叉树
速学路径
http://blog.csdn.net/jiajiayouba/article/details/9224403
树和森林
树的存储结构
双亲表示法
1 |
|
孩子表示法
1 | typedef struct CTNode //孩子结点 |
兄弟表示法
1 | typedef struct CSNode |
树与二叉树的转换
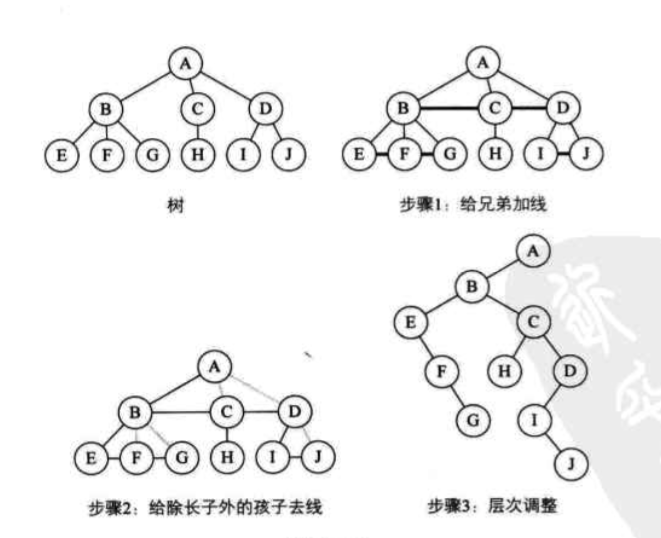
树和森林的遍历
树的遍历
把树转化成二叉树
- 先根遍历(类似于二叉树的先序遍历)
- 后根遍历(类似于二叉树的中序遍历)
森林的遍历
把森林转化成二叉树
- 先序遍历森林(类似于二叉树的先序遍历)
- 中序遍历森林(类似于二叉树的中序遍历)
赫夫曼树
转变二叉树来实现用较小的代价来访问到概率大的元素,又叫最优二叉树
生成最优树的方法
现在有一堆概率数:A:5 , B:15 , C:40 , D:30 , E:10

如上图所示,选两个目前最小的数生成N~1~,保证右子树的权值大于左子树,然后这样循环,即可生成
上图二叉树的带权路径长度(叶子结点的路径之和)
$$
40x1+30x2+15x3+10x4+5x4=205
$$
赫夫曼编码
如下图所示
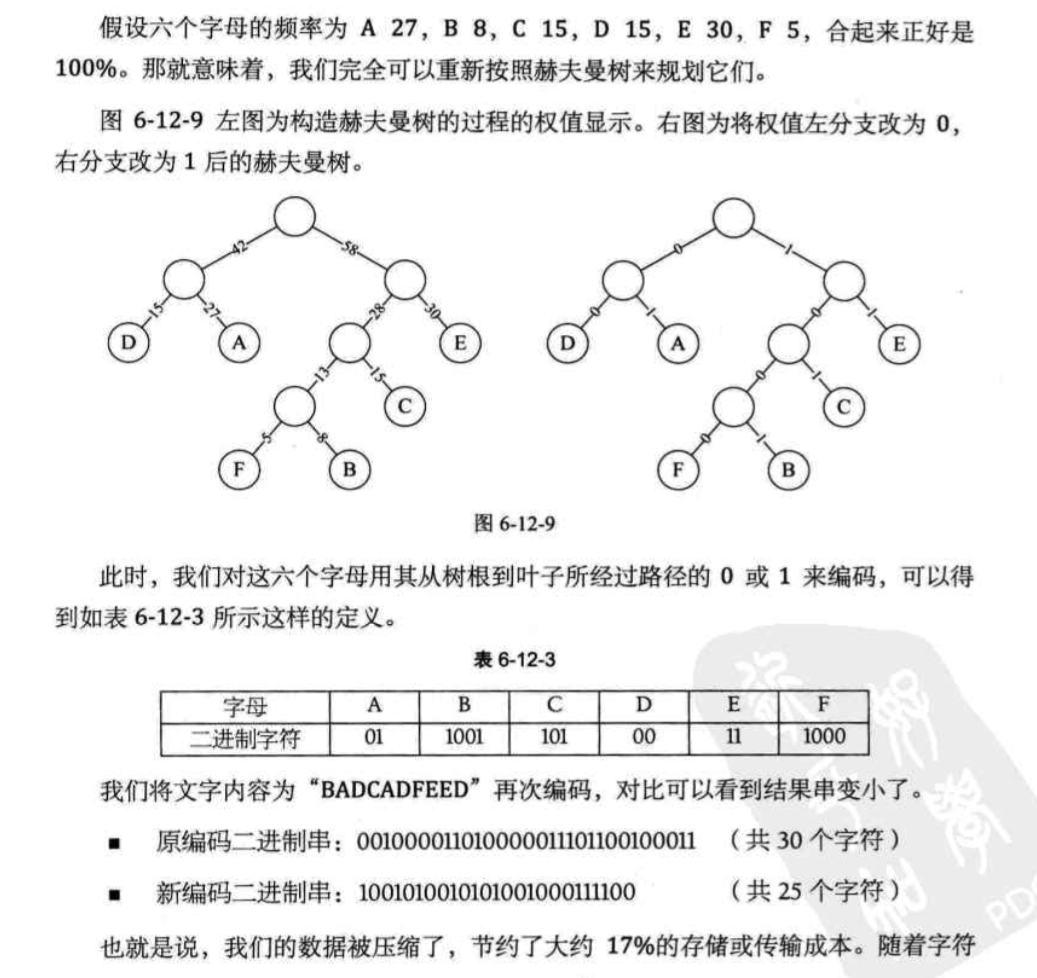
主要思想还是没变,把概率最大的字母用最少的二进制字符来表示,而且每个二进制字符组代表的字母不冲突。
速学路径
http://www.jianshu.com/p/95fba425be44
图
术语
G(V,E)
G表示一个图,V是图的顶点集合,E是图的边集合
无向图
顶点之间的边没有方向
有向图
顶点之间的边有方向,这种边称为有向边,也称为弧
入度
有向边指向顶点V的数量称为入度
出度
有向边离开顶点V的数量称为出度
简单图
不存在顶点到自身的边,并且没有重复的边的图是简单图
网
有权值的图叫做网
连通图
图上任意两个顶点都连通,则为连通图
图的存储结构
邻接矩阵
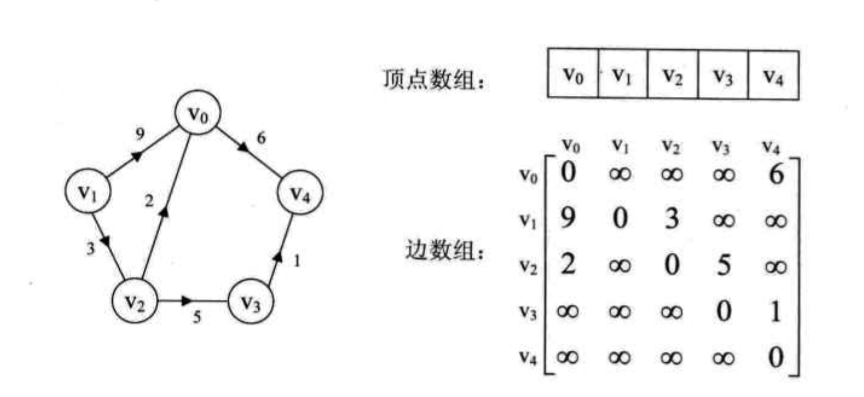
1 | typedef char VertexType; |
邻接表
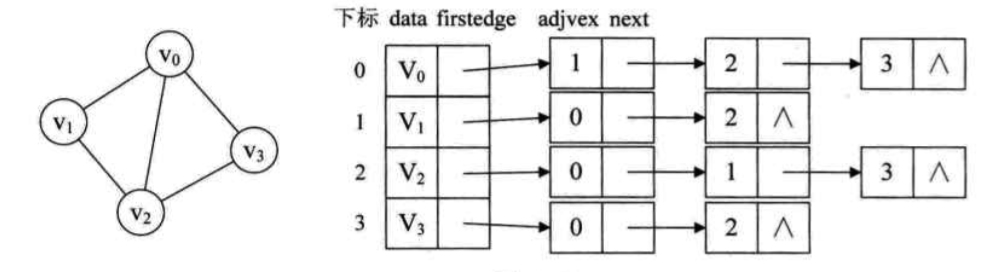
1 |
|
十字链表
邻接表是以出度为出发点,逆邻接表是以入度为出发点,那么十字链表就是结合它们两者
顶点结点
| 指向该顶点的入边表的第一个结点 | 数据 | 指向该顶点的出边表的第一个结点 |
|---|---|---|
| firstin | data | firstout |
弧结点
| 弧起点的下标 | 弧终点的下标 | 指向终点相同的下一条弧 | 指向起点相同的下一条弧 | 数据 |
|---|---|---|---|---|
| tailvex | headvex | hlink | tlink | data |
邻接多重表
是无向图的另一种链式存储结构
图的遍历
深度优先遍历
一直递归地遍历第一个顶点的第一个邻接点,直到访问的顶点没有邻接点后,再对第一个顶点的第二个邻接点进行递归遍历,如此循环
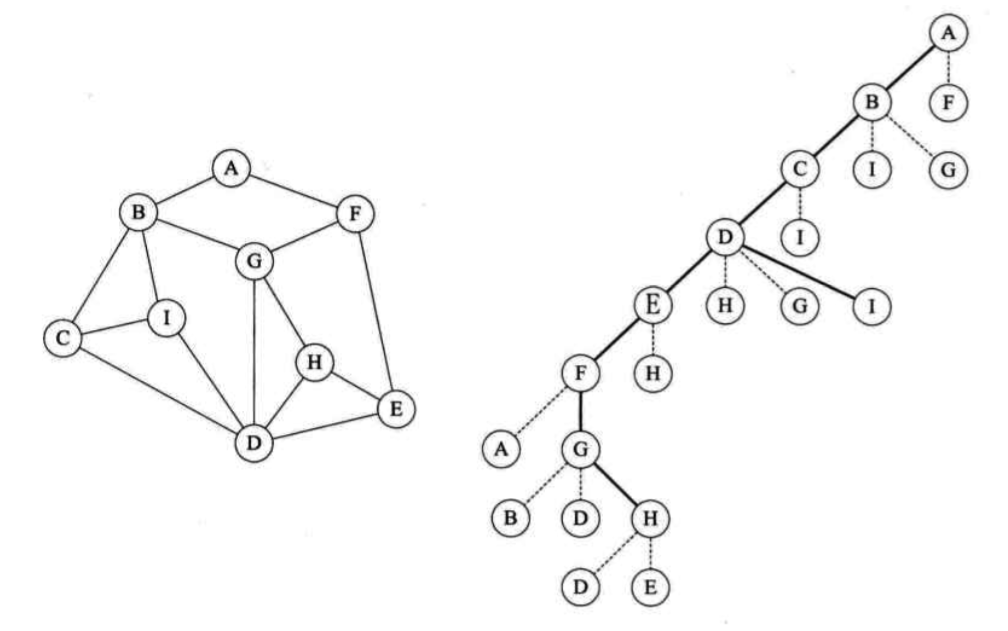
广度优先遍历
以顶点为起始点,由近至远,依次访问和顶点路径想通且路径长度分别为1,2……的顶点
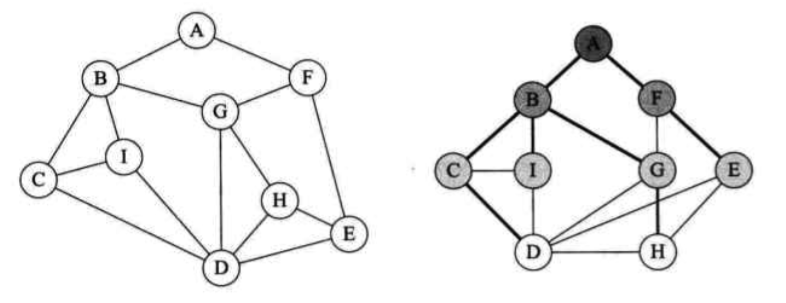
速学路径
http://blog.csdn.net/dreamzuora/article/details/51137132
最小生成树
把各个顶点连接起来的最小代价的树
普里姆(Prim)算法
新建一个集合,放入一个顶点,然后选出和这个顶点连通的最短路径的那个顶点,也放进这个集合,然后选出和这两个顶点连通的最短路径的那个顶点,然后再把它放进集合,直到所有的顶点都在集合里了,那最小生成树也出来了
克鲁斯卡尔(Kruskal)算法
将图中边按其权值由小到大的次序顺序选取,然后凑出来
速学路径
http://blog.csdn.net/weinierbian/article/details/8059129/
拓扑排序
由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步,直到不存在入度为0的顶点为止。
(1) 选择一个入度为0的顶点并输出之;
(2) 从网中删除此顶点及所有出边。
循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列。
AOV网
在有向图中若以顶点表示活动,有向边表示活动之间的先后关系,这样的图简称为AOV网
关键路径
从源点到汇点的路径长度(各路径上持续时间之和)最长的路径叫关键路径
AOE网
用顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间的有向图叫AOE网
最短路径
迪杰斯特拉(Dijkstra)算法
按路径长度递增的次序产生最短路径的算法

速学路径
http://blog.csdn.net/qq_34845121/article/details/62056089
弗洛伊德(Floyd)算法
速学链接
http://blog.csdn.net/bjtu_dubing/article/details/50333027
查找
术语
关键字
是数据元素中某个数据项的值,用它可以标识一个数据元素
顺序查找
从第一个或者最后一个记录开始,逐个与给定的值进行匹配
折半查找
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
时间复杂度为O(logn)
1 | // while循环 |
java实现
1 | public class binarySearch { |
binary search tree
中文翻译可为(排序二叉树,二叉搜索树,二叉查找树)
左子树上的所有结点的值均小于它的根结点的值
右子树上的所有结点的值均大于它的根结构的值
它的左右子树也分别为二叉排序树
把无序序列转成二叉排序树之后,用中序遍历的方法可以输出有序的顺序序列
排序
1 | /** |
1 | /** |
速学路径
http://www.itdadao.com/articles/c15a205949p0.html
B树(B-树,B-tree)
B树是多路平衡查找树,B树每个结点可以有n个元素和n+1个孩子,减少树的高度,所以可以降低内存读取外存的次数;( 对二叉查找树的改进。它的设计思想是,将相关数据尽量集中在一起,以便一次读取多个数据,减少硬盘操作次数)一般用于数据库系统中

性质
- 根结点的儿子数为[2, M]
- 除根结点以外的非叶子节点的儿子数为[M/2, M]
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字
- 每个节点的关键字比它的子节点个数少 1 (叶结点除外)
- 所有的叶子结点都在同一个层级
速学路径
http://www.jianshu.com/p/ed76dbc0536d
B+树
B+树是B树的变种树,有n棵子树的节点中含有n个关键字,每个关键字不保存数据,只用来索引,数据都保存在叶子节点。是为文件系统而生的。

为什么数据库索引采用B+树
因为从磁盘读到内存需要花很多时间,所以普通的搜索树的深度很深,会导致IO时间很长,所以用深度低的多路查找树。那为什么真实数据不放在内层节点呢,是要让磁盘块能放更多的数据项,同时数据项(索引字段)要小一点,这样可以减低树的高度。
区别
重点:B树必须用中序遍历的方法按序扫库, 而B+树直接从叶子结点挨个扫一遍就完了
| B 树 | B+ 树 | |
|---|---|---|
| 关键字 | 关键字分布在整颗树中,只出现一次 | 所有关键字都出现在叶节点的链表中,且有序 |
| 搜索命中 | 可能在树中任意节点命中,搜索结束 | 只可能在叶节点中命中,查询路径稳定 |
| 非叶节点 | 非叶节点包含关键字,也包含数据 | 非叶节点相当于索引帮助搜索到叶节点,叶节点相当于存储关键字数据的数据层 |
| 叶节点 | 增加了链表指针,相当于存储关键字数据的数据层 |
索引
InnoDB和MyISAM的索引区别
MyISAM索引文件和数据文件是分离的,索引文件仅保存数据的地址
InnoDB中,数据文件本身就是按B+Tree组织的一个索引结构,它的叶节点就保存了完整的数据
优缺点
优点
- 大大加快数据的检索速度;
- 创建唯一性索引,保证数据库表中每一行数据的唯一性;
- 加速表和表之间的连接;
- 在使用分组和排序子句进行数据检索时,可以显著减少查询中分组和排序的时间。
缺点
- 索引需要占物理空间。
- 当对表中的数据进行增加、删除和修改的时候,索引也要动态的维护,降低了数据的维护速度。

索引优化
- 如果是联合索引,则把=放在最前面,范围<>between放在最后,因为从左往右匹配
- 有了’AB’索引,就不用’A’索引了
- 索引列匹配的时候,索引不要参与计算
- 索引项尽量小
- 数据量小的表不要建索引
- 索引不是越多越好,因为数据的变更(增删改)都需要维护索引,而且更多的索引意味着也需要更多的空间
- 索引值太单一,比如性别,就不要建索引
- 更新非常频繁的数据也不要建索引
以下情况没有索引效果
- Like “%xxx”,Like的参数不能以通配符开头
- not in , !=
- 对列进行函数运算的情况(如 where md5(password) = “xxxx”)
- WHERE index=1 OR A=10
- int类型的数据 不好做索引
速学路径:
http://www.cnblogs.com/zlcxbb/p/5757245.html
平衡二叉树(AVL树)
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
平衡因子
将二叉树上结点的左子树深度减去右子树深度的值,也只能是-1,0,1
速学路径
http://www.jianshu.com/p/db5529e91f4b
红黑树
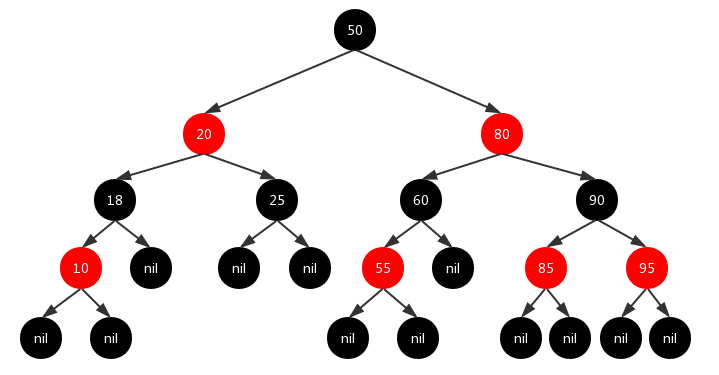
特点
- 每个节点要么是红色,要么是黑色。
- 根节点必须是黑色
- 红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)。
- 对于每个节点,从该点至
null(树尾端)的任何路径,都含有相同个数的黑色节点。 - 每个空叶子节点必须是黑色的;
速学路径
http://www.jianshu.com/p/f4639d0cc887
http://www.importnew.com/21818.html
http://www.importnew.com/21822.html
http://www.jianshu.com/p/23b84ba9a498
哈希表
线性探测法
http://blog.csdn.net/shangruo/article/details/8491733
二次探测法
http://blog.csdn.net/xyzbaihaiping/article/details/51607770

排序
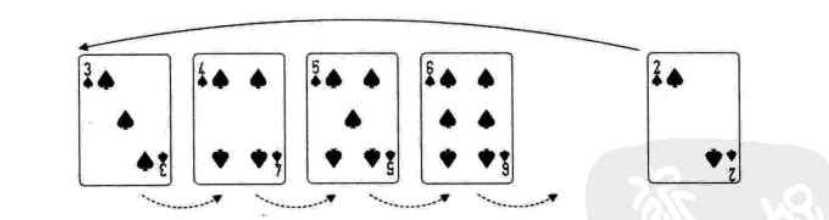
直接插入排序
每步将一个待排序的记录,按其顺序码大小插入到前面已经排序的字序列的合适位置(从后向前找到合适位置后),直到全部插入排序完为止。
1 | void InsertSort(SqList *L) |
java实现
1 | public static void insertSort(int[] list) |
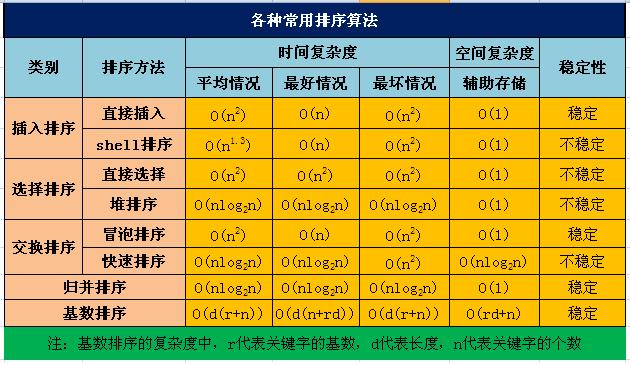
时间复杂度为O[n^2^]
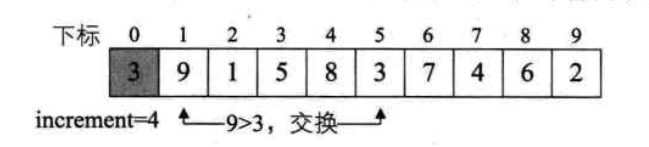
希尔排序
有间隔的直接插入排序
1 | void ShellSort(SQLite *L) |
java实现
1 | public void shellSort(int[] data) |
当n无穷大的时候,可以减少到n(log~2~n)^2^
快速排序
选择一个基准,将比起大的数放在一边,小的数放到另一边。对这个数的两边再递归上述方法。
1 | void sort(int *a, int left, int right) |
java实现
1 | public void sort(int[] list, int start, int end) |
最好情况是O(nlogn),最差情况是O(n^2^)且不稳定
选择排序
n-1次的循环比较,然后选出最小数的下标,然后进行交换
1 | void SelectSort(SQList *L) |
java写法
1 | public static void selection_sort(int[] arr) { |
冒泡排序
- 比较相邻的元素。 如果第一个比第二个大,就交换他们两个。
- 从开始第一对到结尾的最后一对,每对相邻元素都作同样的工作,。 这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
用C写一个冒泡排序
1 | void bubble(int r[n]) |
用Java写一个冒泡排序
1 | import java.util.Comparator; |
1 | import java.util.Comparator; |
堆排序
大顶堆:每个结点的值都大于等于其左右孩子结点的值
小顶堆:每个结点的值都小于等于其左右孩子结点的值
将待排的序列构成一个大顶堆,然后取走堆顶(最大值),然后再调整大顶堆,再取走堆顶,如此往复
每次取走堆顶后,把堆顶替换成之前最后的那个元素,然后再重新排序
最好和最差的情况都是O(nlogn)但不稳定
1 | public static void sort(int[] a){ |
速学路径
http://blog.csdn.net/xiaoxiaoxuewen/article/details/7570621/
http://www.cnblogs.com/kkun/archive/2011/11/23/2260286.html
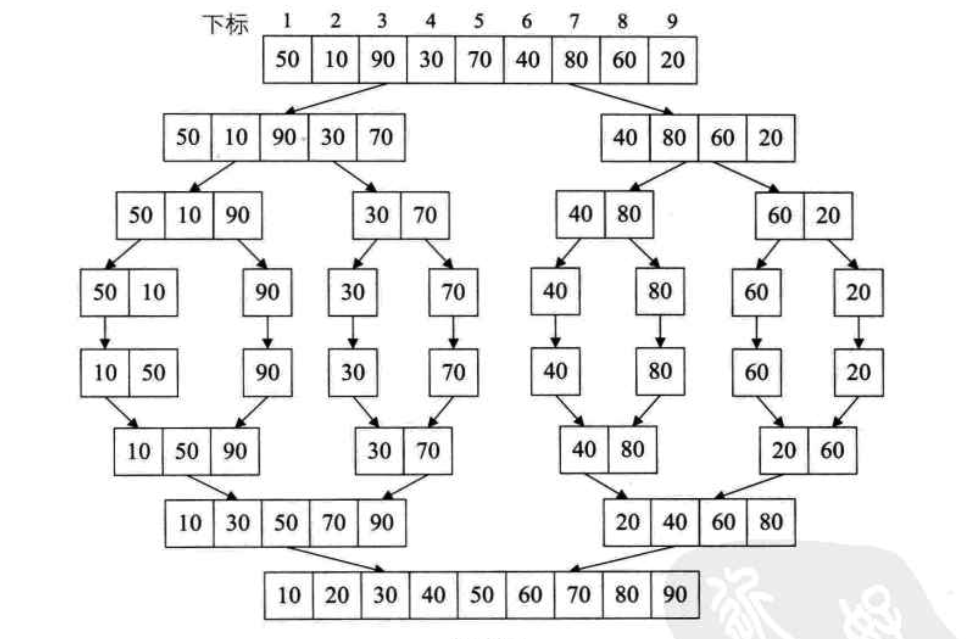
归并排序
把n个有序的子序列两两归并,直到归并成一个序列
最好和最差的情况都是O(nlogn)但稳定
1 | public int[] gb_sort(int[] nums, int low, int high) { |
速学路径
http://blog.csdn.net/yinjiabin/article/details/8265827/
基数排序
从序列的个位开始排列,然后到十位开始排列,直到最高的位数
最好和最坏的情况都是O(d(n+rd))
1 | public void radix_sort(int[] array){ |
速学路径
http://blog.chinaunix.net/uid-26722078-id-3668671.html
http://www.cnblogs.com/kkun/archive/2011/11/23/2260275.html
各类算法比较