算法练习(不断更新中)

发表于 | 更新于 | 分类于

链表

求链表环的入口结点

先用快慢指针判断是否为环，然后快慢指针相交的点就是在环内，然后让慢指针不动，快指针到起点改为每次一步，慢指针也每次一步，继续遍历，（更麻烦的方法：然后再走一圈环回到相交点，就是这个环的长度。有了环的长度，则让两个指针相隔这个长度，然后前进，一旦后一个指针进入环，这两个指针就一定会相遇。）相遇的这个点就是入口结点

数组

一个排好序的数组，找出两数之和为m的所有组合

从数组两边进行推进，如果两数之和小就把前指针往后移，反之也如此，直到找到之后，就可以两边同时缩紧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function find( array, m ) {
  var i = 0;
  var j = array.length - 1;
  var ret = [];
  while( i <= j ) {
    var sum = array[i] + array[j];
    if ( sum > m ) {
      j--;
    }
    else if ( sum < m ) {
      i++;
    }
    else {
      ret.push( [ i, j, array[i], array[j] ] );
      i++;
      j--;
    }
  }
  return ret;
}

自然数序列，找出任意连续之和等于n的所有子序列

从0开始累加，如果到一个点累加的值比n大，就把这个累加数组从最小开始循环移出元素，直至找到匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
lst = [0,2,4,5,3,1,8,6,4,7,9,3,2]

total_sum = 9

def sum_seq(lst):
    seq = []
    ct = 0
    for x in lst:
        seq.append(x)
        ct += x
        if ct == total_sum:
            print seq
            continue
        if ct < total_sum:
            continue
        if ct > total_sum:
            seq_len = len(seq)
            for i in range(seq_len):
                tr = seq.pop(0)
                ct -= tr
                if ct < total_sum:
                    break
                if ct == total_sum:
                    print seq

sum_seq(lst)

判断数组内是否有重复元素

总体思想都是利用额外的数据结构的方式减少时间复杂度，比如辅助数组和哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//第一种
//利用js对象是字典类型的结构(或者Java的Map)，判断是否存在key就好了，时间复杂度为O(n)
function isRepeat(arr){  
     var hash = {};  
     for(var i in arr) {  
         if(hash[arr[i]])  
              return true;  
         hash[arr[i]] = true;  
     }  
     return false;
}

//第二种
//如果数组里都是数字，而且都在一个范围内，那么可以用辅助数组的下标形式判断
//代码略

//第三种
//如果数组里不是数字，那么可以利用HashMap的思想，利用hashcode%数组长度为数组下标+相同hashcode加链表的方式判重
//代码略

//第四种
//先排序，然后判断相邻是否为重复元素，时间复杂度为排序的复杂度
var ary = new Array("111","22","33","111");  
var nary=ary.sort();   
for(var i=0;i<ary.length;i++){    
	if (nary[i]==nary[i+1]){  
		alert("数组重复内容："+nary[i]);
	}  
}

寻找从小到大的第1500个丑数（只包含2，3，5为因子的数是丑数，如4，6，8）

利用空间换时间，保存1500个丑数就好了，关键是如果有序地生成丑数。

因为丑数肯定是丑数*(2,3,5)，我们可以根据已有丑数数组来算，把列表的丑数读乘2，比较是否大于数组里最大的丑数，然后选最小的那个大于数作为后一位丑数，如果都小于，则再试乘3，一次类推

求连续子数组的的最大和，数组里面有正数也有负数。如{1,-2,3,10,-4,7,2,-5}中和最大的子数组是{3,10,-4,7,2}

问题的原型好像就是找出一段和最大的数组。我们可以先从起点开始，保持一个最大数，一直累加，如果累加后一位的时候，发现是负数，则还是保持之前的最大数，如果累加得到的值比当前这个数还小，则累加起点变成这个点，然后最大数变成这个数的值。

树

求二叉查找树中的两个结点的最低公共祖先

从上往下进行遍历，如果结点的值比这两个结点都大或小，则进入他的左子树或右子树，然后如果碰到的结点大小刚好在两个结点的中间，则这个结点就是最低公共祖先。如果遇到刚好等于其中一个结点的值，那么这个结点就是最低公共祖先

求普通二叉树的两个结点的最低公共祖先

既然不是排序树，则判断是否有指向父节点的指针，如果有，可以转化为链表求第一个公共节点的问题；如果还是没有指向父节点的指针，用两个链表分别保存从根节点到输入的两个节点的路径，然后把问题转换成两个链表的最后公共节点

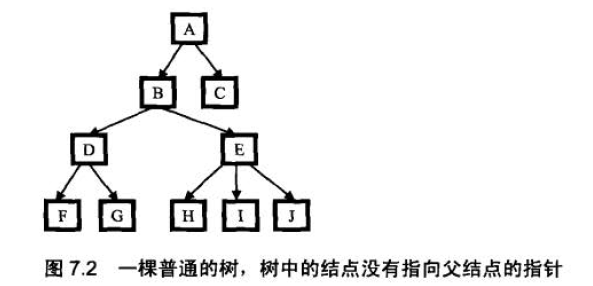
我们首先得到一条从根结点到树中某一结点的路径，这就要求在遍历的时候，有一个辅助内存来保存路径．比如我们用前序遍历的方法来得到从根结点到H的路径的过程是这样的：（ 1 ）遍历到A，把A 存放到路径中去，路径中只有一个结点A; ( 2 ）遍历到B，把B 存到路径中去，此时路径为A->B; ( 3 ）遍历到D，把D 存放到路径中去，此，时路径为A->B->D; ( 4 ） ：遍历到F，把F 存放到路径中去，此时路径为A->B->D->F;( 5) F 已经没有子结点了，因此这条路径不可能到这结点H. 把F 从路径中删除，变成A->B->D; ( 6 ）遍历G. 和结点F 一样，这条路径也不能到达H. 边历完G 之后，路径仍然是A->B->D; ( 7 ）由于D 的所有子结点都遍历过了，不可能到这结点H，因此D 不在从A 到H 的路径中，把D 从路径中删除，变成A->B; ( 8 ）遥历E，把E 加入到路径中，此时路径变成A->B->E, ( 9 ）遍历H，已经到达目标给点， A->B->E 就是从根结点开始到达H 必须经过的路径。

从上到下打印二叉树

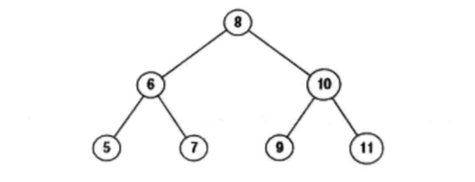
效果如下

1
2
3
8
6 10
5 7 9 11

利用栈的思想，压入从左到右，从上到下的结点，再保持两个变量，一个是下层要打印的节点数，一个是当前层要打印的结点数。比如顶点8，先压栈8，打印后，8出栈，此层打完了就打换行符，再压栈6和10。接着打印6，压栈5和7，6出栈，再打印10，压栈9和11，10出栈，最后打印5，7，9，11

循环

十进制转十六进制

先算出他有几个16次方，然后每次都转换成一个十六进制符号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static String toHex(int num, int base) {
    int divisor = 1;
    char[] table = "0123456789ABCDEF".toCharArray();
    StringBuilder result = new StringBuilder("");
    while (divisor * base <= num) {
        divisor *= base;
    }
    for (; divisor >= 1; divisor /= base) {
        result.append(table[num/divisor]);
        num %= divisor;
    }
    return result.toString();
}

public static void main(String[] args) {
    System.out.println(toHex(1220,16));
}

十六进制转十进制

从字符串的头开始算，然后每次都乘转换数，比如16，然后累加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static int stoi(String src, int base) {
    int digit, result = 0;
    for (int i = 0; i < src.length(); i++) {
        char c = src.charAt(i);
        if (c >= 'a') {
            digit = c - 'a' + 10;
        } else if (c >= 'A') {
            digit = c - 'A' + 10;
        } else {
            digit = c - '0';
        }
        result = base*result + digit;
    }
    return result;
}

public static void main(String[] args) {
    System.out.println(stoi("4C4",16));
}

约瑟夫环问题：已知n个人（以编号1，2，3…n分别表示）围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列，求出列人的顺序编号

关键在于获取每次出列的人的index，其实index=startNum+countNum（开始的序号‘‘0~1’’+规定的长度-1），如果index大于列表总长了，就要用%取余，获取到index后，就remote它，接着开始的序号就变成刚刚remote的index了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
   
public class Yue {  
    public static void main(String[] args) {  
//        Scanner scanner = new Scanner(System.in);  
//        System.out.print("请输入总人数：");  
//        int totalNum = scanner.nextInt();  
//        System.out.print("请输入报数的大小：");  
//        int cycleNum = scanner.nextInt();  
//        System.out.print("请输入开始编号：");  
//        int  startNO= scanner.nextInt();  
//        yuesefu(totalNum, cycleNum,startNO);  
        yuesefu(5, 2,3);  
    }  
   
   public static void yuesefu(int totalNum, int countNum,int startNO) {  
        // 初始化人数  
        List<Integer> start = new ArrayList<Integer>();  
        for (int i = 1; i <= totalNum; i++) {  
            start.add(i);  
        }  
        //从下标为K开始计数  
        int k = startNO-1;  
        while (start.size() >0) {  
            System.out.println(start);
            //第m人的索引位置
            k = (k + countNum) % (start.size()) - 1;  
           // 判断是否到队尾  到队尾时候k=-1
            if (k < 0) {  
                System.out.println(start.get(start.size()-1));  
                start.remove(start.size() - 1);  
                k = 0;  
            } else {  
                System.out.println(start.get(k));  
                start.remove(k);  
            }  
        }  
    }  
}

参考路径

http://www.jianshu.com/p/8e794879dd29

递归

求找钱的所有方法数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static int findNum(int[] arr, int aim){
    if (arr == null || arr.length == 0 || aim == 0){
        return 0;
    }
    return process(arr, 0, aim);
}
//通过递归来切换arr的index，内部循环来进行枚举
public static int process(int[] arr, int index, int aim){
    int num = 0;
    if (index == arr.length){
        num = aim == 0 ? 1 : 0;
    }else {
        for (int i = 0; arr[index] * i <= aim; i++){
            num += process(arr, index + 1, aim - arr[index]*i);
        }
    }
    return num;
}
public static void main(String[] args){
    int[] arr = {5,10,25,1};
    int aim = 15;
    System.out.println(findNum(arr,aim));
}

汉诺塔

汉诺塔有3个柱子，求把n个叠在左侧的塔全移到右侧和搬运的次数，要求一次只能移一个塔，并且小的不能在大的下面

通过递归的方式，寻找抽象的动作，每次都有一个起点，暂放点和重点，可以抽象地从搬多个可以递归到搬一个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static int hanoi(int n){
    if (n > 0){
        return move(n, "left", "right", "mid");
    }
    return 0;
}
public static int move(int n, String from, String to, String helper){
    int num = 0;
    if (n == 1){
        System.out.println(from + " move to " + to);
        return 1;
    }
    num += move(n-1, from, helper, to);
    System.out.println(from + " move to " + to);
    num ++;
    num += move(n-1, helper, to, from);
    return num;
}
public static void main(String[] args) {
    System.out.println(hanoi(3));
}

深度优先遍历

假设在一个9 × 9的格子里，每一步可以往正上、正下、正左、正右、左上、左下、右上、右下八个方向走，但是空白区域不能走，走过的点不能再走。求能吃最多果实的路线。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class Pos {
    private int x;  // 横坐标
    private int y;  // 纵坐标

    // get、set、construct方法省略

    @Override
    public String toString() {
        final StringBuffer sb = new StringBuffer("Pos{");
        sb.append("x=").append(x);
        sb.append(", y=").append(y);
        sb.append('}');
        return sb.toString();
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;

        Pos pos = (Pos) o;

        return x == pos.x && y == pos.y;
    }

    @Override
    public int hashCode() {
        int result = x;
        result = 31 * result + y;
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
public class Sdbl {

    /**
     * 通过深度优先搜索算法获取最长路径
     *
     * @param map        地图
     * @param start      起点
     * @param moveOffset 移动偏移量
     * @return 最长路径
     */
    public static List<Pos> getLongestPathByDFS(int[][] map, Pos start, Pos[] moveOffset) {

        List<Pos> longestPath = new ArrayList<>();
        dfs(start, map, new ArrayList<>(), longestPath, moveOffset);
        return longestPath;

    }

    /**
     * 递归实现深度优先搜索
     */
    private static void dfs(Pos pos, int[][] map, List<Pos> oldPath, List<Pos> result, Pos[] moveOffset) {

        // 记录当前位置向周围格子移动的记录
        List<Pos> visited = new ArrayList<>();

        // 依次向周围移动
        for (Pos aMoveOffset : moveOffset) {
            Pos next = new Pos(pos.getX() + aMoveOffset.getX(), pos.getY() + aMoveOffset.getY());

            if (inMap(map, next) && !oldPath.contains(next) && map[next.getX()][next.getY()] == 1) {
                oldPath.add(next);
                visited.add(next);
                dfs(next, map, oldPath, result, moveOffset);
            }
        }

        // 若在当前位置下，没有向周围的格子移动过时，保存最长路径
        if (visited.isEmpty()) {
            if (oldPath.size() > result.size()) {
                result.clear();
                result.addAll(oldPath);
            }
        }

        // 周围的格子都不可以移动时回退到上一格子
//        for (Pos neighbour : neighbours) {
//            if (canPath(map, oldPath, neighbour, visited)) {
//                System.out.println("我到了 "+neighbour);
//                return;
//            }
//        }
        oldPath.remove(pos);

    }

    /**
     * 判断格子是否可以移动
     */
    private static boolean canPath(int[][] map, List<Pos> path, Pos pos, List<Pos> visited) {

        // 不在地图里，不能移动
        if (!inMap(map, pos)) {
            return false;
        }

        // 空白格子，不能移动
        if (map[pos.getY()][pos.getX()] == 0) {
            return false;
        }

        // 已经在路径中或经过，不能移动
        if (path.contains(pos) || visited.contains(pos)) {
            return false;
        }

        return true;
    }

    /**
     * 判断格子是否在地图内
     */
    private static boolean inMap(int[][] map, Pos pos) {

        if (pos.getY() < 0 || pos.getY() >= map.length) {
            return false;
        }

        if (pos.getX() < 0 || pos.getX() >= map[0].length) {
            return false;
        }

        return true;

    }


    public static void main(String[] args) {

        // 初始化参数
        int[][] simpleMap = new int[][]{
                {0, 0, 0, 0, 0, 0, 0, 0, 0},
                {0, 0, 0, 0, 0, 0, 0, 0, 0},
                {0, 0, 0, 1, 0, 0, 0, 0, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0},
                {0, 0, 0, 1, 0, 1, 0, 0, 0},
                {0, 0, 0, 0, 1, 1, 0, 0, 0},
                {0, 0, 0, 0, 0, 0, 0, 0, 0}
        };

        Pos[] moveOffset = new Pos[]{
                new Pos(-1, 0),    // 向左移动
                new Pos(-1, -1),    // 向左上移动
                new Pos(0, -1),    // 向上移动
                new Pos(1, -1),    // 向右上移动
                new Pos(1, 0),    // 向右移动
                new Pos(1, 1),    // 向右下移动
                new Pos(0, 1),    // 向下移动
                new Pos(-1, 1)     // 向左下移动
        };
        Pos start = new Pos(3, 3);

        // 执行深度优先算法
        List<Pos> longestPath = getLongestPathByDFS(simpleMap, start, moveOffset);

        // 打印路径
        System.out.println(longestPath);

    }
}

动态规划

你正在爬n层的楼梯，但每次你只能爬一步或者两步，你能有多少种不同的方法爬到楼顶部？

已知爬1层和2层的方法数，在前面的基础上，可以知道爬3层的数方法数，同理4层只能是通过2层的基础+2步或3层的基础+1步来实现的，而前面已经知道2层和3层的方法数了，相加就好了，这个是动态规划的思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function climb(floor){
	if(floor < 1){
		return 1;
	}

	var plans = [];

	plans[1] = 1;
	plans[2] = 2;

	for(var cur = 3; cur <= floor; cur++){
		plans[cur] = plans[cur - 1] + plans[cur - 2];
	}

	return plans[floor];
}

矩阵求从[0,0]路径[3,3]点的最小值

1
2
3
4
2 5 4 8
1 4 2 6
9 2 5 7
0 2 8 2

先求上面一行和左边一行的路径最小值

2 7 11 19
3
12
12

然后可以开始遍历剩余的点，左边和上边选一个最小值，再加上自己的值就是这个点的最小路径值，直到遍历到[3,3]点

最长递增子序列（不连续）

先从末尾分析，如果n位大于n-1位，则dp(n) = dp(n-1)+1，然后从0位开始积累dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static int lis(int[] arr){
    int maxLength = 1;
    //例如dp[3]是前4位序列包含的最长递增子序列的值
    int[] dp = new int[arr.length];
    //第一个数，自己是自己的最长递增子序列，初始值为1
    dp[0] = 1;
    for (int i = 1; i < arr.length; i++) {
        //不去考虑之前的值，的确初始值为1
        dp[i] = 1;
        for (int j = i - 1; j >= 0; j--) {
            //找出前面dp大于当前dp的位置 并且 要求之前序列的最后位的值小于当前值才符合条件
            if (dp[j] >= dp[i] && arr[j] < arr[i]) {
                dp[i] = dp[j] + 1;
                System.out.println("d["+i+"] 找前面的值是:d["+j+"]");
            }
              //if (arr[j] < arr[i]) {
              //  dp[i] = dp[j] + 1;
              //  System.out.println("d["+i+"] 找前面的值是:d["+j+"]");
              //  break;
              //}
        }
        if (dp[i] > maxLength) {
            maxLength = dp[i];
        }
    }
    return maxLength;
}

最长公共子序列（不连续）

从末尾分析，如果X[i]==Y[j]，则c[i][j] = c[i-1][j-1]+1;如果X[i]!=Y[j]，则c[i][j] = Math.max(c[i][j-1],c[i-1][j])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static int[][] lengthofLCS(char[] X, char[] Y){
    /* 构造二维数组c[][]记录X[i]和Y[j]的LCS长度 (i,j)是前缀
     * c[i][j]=0; 当 i = j = 0;
     * c[i][j]=c[i-1][j-1]+1; 当 i = j > 0; Xi == Y[i]
     * c[i][j]=max(c[i-1][j],c[i][j+1]); 当 i = j > 0; Xi 
     * 需要计算 m*n 个子问题的长度 即 任意c[i][j]的长度
     * -- 填表过程
     */
    int[][]c = new int[X.length+1][Y.length+1];
    // 动态规划计算所有子问题
    for(int i=1;i<=X.length;i++){
        for (int j=1;j<=Y.length;j++){
            if(X[i-1]==Y[j-1]){
                c[i][j] = c[i-1][j-1]+1;
            }else{
                c[i][j] = Math.max(c[i][j-1],c[i-1][j]);
            }
        }
    }
    // 打印C数组
    for(int i=0;i<=X.length;i++){
        for (int j=0;j<=Y.length;j++){
            System.out.print(c[i][j]+" ");
        }
        System.out.println();
    }
    return c;
}

最长公共子串（连续）

和上面的基本一样，但是如果X[i]!=Y[j]，则c[i][j]为0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public  static int lengthofLCString(String X, String Y){
    /* 构造二维数组c[][]记录X[i]和Y[j]的LCS长度 (i,j)是前缀
     * c[i][j]=0; 当 i = j = 0;
     * c[i][j]=c[i-1][j-1]+1; 当 i = j > 0; Xi == Y[i]
     * c[i][j]=0; 当 i = j > 0; Xi != Y[i]
     * 需要计算 m*n 个子问题的长度 即 任意c[i][j]的长度
     * -- 填表过程
     */
    int[][]c = new int[X.length()+1][Y.length()+1];
    int maxlen = 0;
    for(int i =1;i<=X.length();i++){
        for(int j=1;j<=Y.length();j++){
            if(X.charAt(i-1) == Y.charAt(j-1)){
                c[i][j] = c[i-1][j-1]+1;
                if(c[i][j] > maxlen)
                {
                    maxlen = c[i][j];
                }
            }
        }
    }
    return maxlen;
}

设dp是走到这一步最少要有的血量，先算出最后一行的dp，然后在从下遍历到上一行，因为每一个点的dp是依赖于正下和右边的dp的，所以遍历结束，就知道了dp[0][0]需要多少的初始血量了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static int minHP(int[][] m){
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0){
        return 1;
    }
    int row = m.length;
    int col = m[0].length;
    int[][] dp = new int[row][col];
    dp[row-1][col-1] = m[row-1][col-1] > 0 ? 1 : -m[row-1][col-1] + 1;
    for (int j = col - 2; j >= 0; j--){
        dp[row-1][j] = Math.max(dp[row-1][j+1] - m[row-1][j], 1);
    }
    
    int right = 0;
    int down = 0;
    for (int i = row - 2; i >= 0; i--){
        dp[i][col-1] = Math.max(dp[i+1][col-1] - m[i][col-1], 1);
        for (int j = col - 2; j >= 0; j--){
            right = Math.max(dp[i][j+1] - m[i][j], 1);
            down = Math.max(dp[i+1][j] - m[i][j], 1);
            dp[i][j] = Math.min(right,down);
        }
    }
    return dp[0][0];
}
public static void main(String[] args) {
    int[] m1 = {-2,-3,3};
    int[] m2 = {-5,-10,1};
    int[] m3 = {0,30,-5};
    int[][] n = {m1,m2,m3};
    System.out.println(minHP(n));
}

回溯法

尝试一下，如果失败则回退到之前的逻辑

八皇后

在8*8的棋盘上要求放8个棋子，而且他们互不在同一行同一列同一斜线

先放8个不同的行，然后遍历放列，每次遍历判断是否和之前的不在同一列同一斜线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * 一共有多少个皇后（此时设置为8皇后在8X8棋盘，可以修改此值来设置N皇后问题）
 */
int max = 8;
/**
 * 该数组保存结果，第一个皇后摆在array[0]列，第二个摆在array[1]列
 */
int[] array = new int[max];
public static void main(String[] args) {
    new WolfQueen().check(0);
}
/**
 * n代表当前是第几个皇后
 * @param n
 * 皇后n在array[n]列
 */
private void check(int n) {
    //终止条件是最后一行已经摆完，由于每摆一步都会校验是否有冲突，所以只要最后一行摆完，说明已经得到了一个正确解
    if (n == max) {
        print();
        return;
    }
    //从第一列开始放值，然后判断是否和本行本列本斜线有冲突，如果OK，就进入下一行的逻辑
    for (int i = 0; i < max; i++) {
        array[n] = i;
        if (judge(n)) {
            check(n + 1);
        }
    }
}
private boolean judge(int n) {
    for (int i = 0; i < n; i++) {
        if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
            return false;
        }
    }
    return true;
}
private void print()  {
    for (int i = 0; i < array.length; i++) {
        System.out.print(array[i] + 1 + " ");
    }
    System.out.println();
}